ELECTRÓNICA DIGITAL

ELECTRÓNICA DIGITAL

LA ELECTRÓNICA estudia el comportamiento de los electrones en diversos medios (gases, vacío, conductores y semiconductores), que posibilitan la generación, transmisión, recepción y almacenamiento de información contenida en señales eléctricas y este conocimiento se aplica para diseñar y construir circuitos electrónicos para ello. los electrones se comportan de la forma que nos interesa".

La corriente se puede controlar o regular, según la funcionalidad requerida.

VÍDEOS

CONVERSIÓN DECIMAL A BINARIO	ARITMÉTICA DIGITAL: SUMADORES Y RESTADORES
ÁLGEBRA BOOLEANA: AXIOMAS Y TEOREMAS	MAPAS DE KARNAUGH
INVENTOR DE LA APLICACIÓN: INTRODUCCIÓN	INVENTOR DE LA APLICACIÓN: PRÁCTICA 1

ELECTRÓNICA ANALÓGICA

La electrónica analógica se ocupa del tipo de señales analógicas que existen en el mundo real, modificando sus características (amplificando, atenuando, filtrando…). Trabaja con variables continuas de tal forma que un pequeño cambio en alguna variable puede producir un gran cambio en el comportamiento del circuito. Un ejemplo de estos circuitos puede ser un amplificador de señal.

ELECTRÓNICA DIGITAL

En electrónica digital la señal se describe mediante números (estados). Son los números los que se manipulan , almacenan , recuperan y transportan . Trabajar con variables discretas.

La electrónica digital funciona con números. La información está en números y no en forma de señal. Cualquier señal siempre se puede convertir a números y recuperar más tarde .

CIRCUITO HÍBRIDO

EL TÉRMINO “ANALOGICO” se refiere a magnitudes o valores que varían con el tiempo de manera continua, como la distancia y la temperatura, la velocidad, que podrían variar muy lentamente o muy rápidamente como un sistema de audio.

EL TÉRMINO "DIGITAL" se refiere a cantidades discretas como la cantidad de personas en una habitación, la cantidad de libros en una biblioteca, la cantidad de autos en un estacionamiento, etc.

En la tecnología analógica es muy difícil almacenar, manipular, comparar, calcular y recuperar información con precisión cuando ha sido guardada, en cambio en la tecnología digital (computadoras) las tareas se pueden realizar de manera muy rápida, exacta, precisa y sin detenerse.

ELECTRÓNICA DIGITAL : Es  una ciencia que estudia señales eléctricas discretas, con dos niveles de voltaje: estado alto ( High) o Uno lógico; y otro, de estado bajo ( Low ) o Cero Lógico.

LÓGICA POSITIVA

En esta notación, el " 1" lógico corresponde al nivel de voltaje más alto (positivo) y el " 0"  lógico corresponde al nivel más bajo (negativo).

LÓGICA NEGATIVA

Representa el estado "1" con los niveles de voltaje más bajos y el estado "0" con los niveles más altos.

ACTIVIDAD: INTRODUCCIÓN A LA ELECTRÓNICA DIGITAL

SISTEMAS NUMÉRICOS

CONVERSIONES ENTRE SISTEMAS

Hay dos métodos de conversión básicos: polinómico e iterativo.

El método polinómico consiste en expresar el número de la base de origen como un polinomio y evaluarlo según la aritmética de la base de destino.  

El método iterativo consiste en dividir el número (utilizando la aritmética de la base de origen) por la base de destino de tal forma que el resto nos dará los dígitos de la nueva base, siendo el más significativo el último dígito obtenido.

CONVERSIÓN DECIMAL A BINARIO

MÉTODO DE DIVISIONES SUCESIVAS

MÉTODO POR DESCOMPOSICIÓN Y RESIDUOS

MÉTODO CERCANO A LA POTENCIA

CONVERSIÓN BINARIO A DECIMAL

MÉTODO DE MULTIPLICACIONES DE SUCESIÓN

MÉTODO DE SUMAS SUCESIVAS

CONCLUSIÓN :

• Para convertir de DECIMAL a cualquier otro sistema numérico aplica el método de divisiones sucesivas en la base que quieras llegar.

• Para convertir de cualquier sistema a DECIMAL, luego se aplica el método de las multiplicaciones sucesivas, diseñando una tabla de potencias de 2, 8 o 16 según lo que se quiera lograr.

OPERACIONES BINARIAS

SUMA

DESCANSAR

MULTIPLICACIÓN

DIVISIÓN

COMPLEMENTAR

SUMA BINARIA

RESTA BINARIA

MULTIPLICACIÓN BINARIA

DIVISIÓN BINARIA

Si intentas dividir el dividendo entre el divisor, empieza por tomar el mismo número de cifras en ambos. Si no se puede dividir, se toma un dígito más.

Si la división es posible, el divisor sólo puede estar contenido una vez en el dividendo, es decir, el primer dígito del cociente es UNO.

En ese caso, el resultado de multiplicar el divisor por 1 es el divisor mismo. Restamos las cifras del dividendo del divisor y restamos la siguiente cifra.

El procedimiento de división continúa.

Reglas de la división binaria: 

0/0 no permitido; 1/0 no permitido;0/1=0; 1/1=1.

VÍDEO: SISTEMAS NUMÉRICOS

https://youtu.be/YwGs4R5FxvM 

https://www.youtube.com/watch?v=YwGs4R5FxvM&t=12s 

............................................................................................................................................

TALLER DE ARITMÉTICA DIGITAL

COMPETENCIA: Reconocer los diversos sistemas numéricos utilizados en la electrónica digital y las operaciones binarias aplicadas en la tecnología.

Metodología: Aplicando un método adecuado, realizar cada conversión paso a paso.

1) Convierta los siguientes números decimales a binarios:

a) 215	segundo) 63	c) 200	d) 33	mi) 69
f) 77	g) 642	h) 111	yo) 141	i) 88
k) 47	l) 514	m) 217	n) 365	norte) 300

2) Convierta los siguientes números binarios a decimales:

a) (10011) 2	segundo) (101100) 2	c) (11110111) 2	d) (1000000) 2	e) (11001100011) 2
f) (111011110) 2	g) (10001) 2	h) (1001000) 2	yo) (110010011) 2	j) (11111111) 2
k) (10101010) 2	l) (1110111011) 2	metro) (10000) 2	n) (1111101) 2	ñ) (11110000) 2

3) Convierta los siguientes números binarios a octales:

a) (111011) 2	segundo) (1111100) 2	c) (10010100) 2	d) (1001001100) 2	mi) (1101010010) 2
f) (11001) 2	g) (10111010011) 2	h) (1011011001) 2	yo) (100001011) 2	j) (1010110) 2
k) (111011010) 2	l) (1011011101) 2	metro) (1000000010) 2	n) (11111111111) 2	ñ) (10110110010) 2

4) Convierta los siguientes números binarios a hexadecimal:

a) (101111011101) 2	segundo) (101101100101001) 2	c) (100010100000100) 2	d) (1011100111) 2
mi) (101000) 2	f) (1101011011101111) 2	g) (1011011011) 2	h) (1111011110111) 2
yo) (10100101101) 2	j) (110001100101) 2	k) (1000000101) 2	l) (101101110) 2

5) Convierta los siguientes hexadecimales a octal:

a) ( DE4) 16	b) (3A7) 16	c) (1F2E) 16	d) (9A2B8) 16
mi) (7531) 16	f) (1F2E) 16	g) (DD07) 16	h) (36B9) 16
i) (F2CCE) 16	j) (642) 16	k) (C495) 16	l) (5A08) 16
m) (D8539) 16	n) (FF) 16	ñ) (EAE) 16	o) (5070) 16

6) Convierta el siguiente octal a hexadecimal:

a) ( 3463) 8	b) ( 1035) 8	c) ( 3257) 8	d) ( 7147) 8
e) ( 12204) 8	f) ( 71) 8	g) ( 63714) 8	h) ( 7362) 8
yo) ( 47667) 8	j) ( 201037) 8	k) ( 5555) 8	l) ( 77777) 8
m) ( 3571) 8	norte) ( 646202) 8	ñ) ( 43057) 8	o) ( 44) 8

 ................................................ .. ................................................. .... .................................

TALLER DE OPERACIONES BINARIAS

COMPETENCIA:  Reconocer los diversos sistemas numéricos utilizados en la electrónica digital y las operaciones binarias aplicadas en la tecnología.

Metodología: Aplicando un método adecuado se realiza cada operación, paso a paso.

1) Realizar las siguientes sumas (expresar el resultado en hexadecimal)

a) (1000101) 2 + (1011010) 2	segundo) (110110) 2 + (1011011) 2	c) (100010010) 2 + (100110101) 2
d) (101) 2 + (111) 2	e) (1111011) 2 + (1110011) 2	f) (100101) 2 + (100101) 2 + (10111) 2
g) (100110) 2 + (45) 8	h) (101101011110) 2 + (3D4) 16	i) (4510) 8 + (2F5) 16
j) (1011011110101) 2 + (7253) 8 + (D9B) 16	k) (1110111101001101) 2 + (41562) 8 + (A26F) 16

2) Realizar las siguientes restas (expresar el resultado en octal)

a) (1101101) 2 – (111011) 2	b) (10110101) 2 – (100011011) 2	c) (10001) 2 – (1011) 2
d) (110001) 2 – (111010) 2	e) (1001000100) 2 – (111101111) 2	f) (11101) 2 – (1011) 2 – (1101) 2
g) (45) 8 – (101111) 2	h) (10111011) 2 – (B8) 16	i) (6421) 8 – ( 93C ) 16
j) (2357) 8 – (10111110100) 2 – (E8) 16	k) (1111100110101101) 2 – (61425) 8 – (3DF3) 16

3) Realizar las siguientes operaciones (expresar el resultado en hexadecimal)

a) (1011) 2 + (110) 2 – (1001) 2	segundo) (1001) 2 + (1111) 2 – (1011) 2	c) (10000) 2 – (1001) 2 + (101) 2
d) (34) 8 – (27) 8	e) (74) 8 – (65) 8 + (34) 8 – (46) 8	f) (FC) 16 – (9E) 16 + (3B) 16
g) (471) 8 – (E3) 16 + (10001) 2	h) (355) 8 + (DC) 16 – (1000) 8	yo) (3B) 16 – (46) 8 – (33) 8
j) (EA02) 16 – (7451) 8 + (5436) 8	k) (10110101101) 2 – (4213) 8 – (5E9) 16

4) Encuentra el complemento de los siguientes números (exprésalo en la misma base)

a) (100101110) 2	b) (011001) 2	c) (111001001) 2
d) (1340) 8	mi) (54130) 8	f) (2DF4) 16
g) (4DC87) 16	h) (12503) 8	yo) (706734) 8
j) (1001011000101) 2	k) (88887) 16

5) Realiza las siguientes restas usando el complemento de n:

a) (35457) 8 – (26543) 8	b) (630012) 8 – (514666) 8	c) (A240D) 16 – (7B76E) 16
d) ( 3731C ) 16 – (9C3A7) 16	e) (75023) 8 – (74351) 8	f) (DE902) 16 – (F464) 16

  

6) Para cada número a continuación, encuentre el resto de sí mismo menos su complemento:

a) (10011110) 2	segundo) (B4E100) 16	c) (10566) 8	d) (17770) 8
mi) (1000) 16	f) (0777) 8	g) (0011000111) 2	h) (BF85CA) 16

  

7) Realice las siguientes conversiones de unidades informáticas:

a) 16384 bytes a Kb	b) 0,125 Tb a Mb	c) 7700480 bits a Kb	d) 22528 Kb a Mb	e) 0,9375 Gb a Mb	f) 1,0625 Mb en bytes
g) 34603008 bits a Mb	h) 40320 bits a bytes	i) 262144 Kb a Gb	j) 8192 Gb a Tb	k) 131072 Kb en GB	l) 0,0078125 Kb en bits

 ................................................ .. ................................................. .... ................................................ ...... .

CÓDIGO BCD

(Decimal codificado en binario (BCD) o Decimal codificado). Representa números decimales en el sistema binario, donde cada dígito decimal está codificado con una secuencia de 4 bits.

Códigos:

Código BCD : decimal codificado en binario

Código BCD de Aiken

Exceso de código BCD 3

código gris

Conversión binario-gris

Conversión gris-gris

 ................................................ .. ................................................. .... ................................................ ...... .

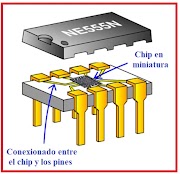
CIRCUITOS INTEGRADOS DIGITALES

 ................................................ .. ................................................. .... ................................................ ...... .

COMPUERTAS DIGITALES

COMPUERTA OR: La salida es "1" cuando CUALQUIERA de las entradas es "1"

COMPUERTA AND: La salida es "1" cuando TODAS las entradas son "1"

NOT GATE: niega el valor de entrada

NOR GATE: La salida es "1" solo cuando todas las entradas son "0"

NAND GATE: La salida es "1" cuando alguna de las entradas es "0"

COMPUERTA YES: Doble negación

COMPUERTA XOR:   La salida es " 1 " cuando las entradas son diferentes

COMPUERTA XNOR:   La salida es " 1 " cuando  las entradas son iguales.

CONEXIÓN DEL DIPSWITCH

COMPUERTA CONECTADA, CON DIPWITCH

IMPLEMENTACIÓN DE PROTOBOARD DE PUERTAS OR, NOT y SÍ

SIMULACIONES CON PUERTAS DIGITALES

SISTEMA ANSI - Instituto Nacional Americano de Estándares

SISTEMA IEC - Comisión Electrotécnica Internacional 

SISTEMA NEMA

-------------------------------------------------- -------------------------------------------------- --------------

VARIAS COMPUERTAS OR

VARIAS COMPUERTAS AND

COMPUERTAS CMOS

COMPUERTAS DE TRES ENTRADAS

:::::::::::::::::::::::::::::::::::::::::::::::::::::::: ::: :::::.::::

COMPUERTAS EQUIVALENTES

:::::::::::::::::::::::::::::::::::::::::::::::::::::::: ::: ::::::::::::::::::::::::::::::::::::::::::::::::::::: :::::: ::::::::::::::::::::::::

ACTIVIDAD 2: COMPUERTAS LÓGICAS

(1). Complete la tabla que se ilustra a continuación:

(2). Según los valores de entrada y el funcionamiento lógico de las compuertas, complete en cada casilla qué valor se obtiene.

(3). Escribe las expresiones algebraicas que corresponden a cada etapa del circuito.

(4). Dibuje la señal del reloj en la salida de cada puerta digital.

(5). Grafique los circuitos lógicos que realizan la función dada.

(6). Complete la tabla de verdad del circuito combinacional dado:

ACTIVIDAD 3. EXPRESIONES ALGEBRAICAS

Escribe las expresiones algebraicas que corresponden a cada etapa del circuito.

En la Electrónica, el Álgebra de Boole es una estructura algebraica que incluye las operaciones lógicas O, Y, NO (OR, AND y NOT), así como el conjunto de operaciones: unión, intersección y complemento. Se denomina así en honor a George Boole, matemático inglés que fue el primero en definirla como parte de un sistema lógico a mediados del siglo XIX. Específicamente, el Álgebra de Boole fue un intento de utilizar las técnicas algebraicas para tratar expresiones de la lógica proposicional.

DEMOSTRACIONES

Simplificar las siguientes expresiones:

(1). A B' D + A B' D'

                           AB'(D + D’) = AB'(1) = AB'

(2).  AB + AB’ =
                            A(B + B’) = A(1) = A 

(3).  A’B’C + AB’C + AB’C + ABC

                            A’B’C + AB’C + ABC’ + ABC

                               B’C(A’+A)  +  AB(C’ + C)

                               B’C(1)  +  AB(1)

                               B’C  +  AB

                            AB + B’C 

(4).  ABC + AC + C 

                           C(AB +  A  + 1) 

                           C(1)

                           C

(5).  AB + A(B + C) + B(B +C)

                           AB + AB + AC + BB + BC

                           AB + AC + B + BC

                           AB + B + BC + AC

                           B(A + 1 + C) + AC

                           B(1) + AC

                           B + AC

(6).  (A + B)(A + B’) 

                         AA + AB’ + AB + BB’

                         A + AB’ + AB

                         A(1 + B’ + B)

                         A(1)

                         A

(7).  AB’(C + BD) + (A’B’)C

               AB’C + AB’BD + A’B’C

                         AB’C  +  A’B’C

                         B’C (A + A’)

                         B’C (1)

                         B’C

(8).  A’B’C + A’BC’ + A’BCD + ABC’ 

                        A’B’C + A’BC + A’BC’ + ABC’

                        A’C(B’+B) + BC’(A’+A)

                        A’C(1) + BC’(1)

                        A’C + BC’     

(9).  ABC + AB’(A’C’)’ + AB’ + AC

(10).  [A+(B'C) + D+(EF)] * [A+(B'C) + (D+(EF))']

Un sistema de alarma está constituido por cuatro (4) detectores denominados A, B, C y D. El sistema debe activarse cuando se accionen TRES o CUATRO detectores. Diseñar el circuito lógico.

.....................................................................................................................................................

VIDEO: ÁLGEBRA DE BOOLE

AXIOMAS, TEOREMAS y DEMOSTRACIONES

VIDEO: https://youtu.be/vsR3CVsN_jk

https://www.youtube.com/watch?v=vsR3CVsN_jk

.......................................................................................................................................................

.....................................................................................................................................................

VIDEO: DISEÑO DIGITAL

DISEÑO DE SUMADORES y RESTADORES

VIDEO: https://youtu.be/KBcxlh2JdDM

https://www.youtube.com/watch?v=KBcxlh2JdDM&t=82s

.......................................................................................................................................................

EJERCICIOS RESUELTOS EN EL DISEÑO DIGITAL

1). Simplificar las siguientes expresiones, hasta la mínima expresión, aplicando los Teoremas del Álgebra de Boole y graficando el circuito digital obtenido.

 

2). A partir de la Tabla de Verdad se obtienen las expresiones booleanas, luego se simplifican y finalmente, se grafica el circuito correspondiente

Un mapa de Karnaugh (también conocido como tabla de Karnaugh o diagrama de Veitch, es un diagrama utilizado para la minimización de funciones algebraicas booleanas. El mapa de Karnaugh fue inventado en 1950 por Maurice Karnaugh un físico y matemático de los laboratorios Bell.

Un Mapa de Karnaugh es una representación gráfica de una función lógica a partir de una tabla de verdad. El número de celdas del mapa es igual al número de combinaciones que se pueden obtener con las variables de entrada. Los mapas se pueden utilizar para 2, 3, 4 y 5 variables. 

ADYACENCIA DE 2, 4 y 8

Mapa de Karnaugh empleando SUMA DE PRODUCTOS (SDP)

La simplificación de expresiones lógicas mediante el mapa de Karnaugh utiliza un método gráfico basado en la Suma de Productos.

......................................................................................................................................

Aplicaciones de los Mapa de Karnaugh 

Un motor eléctrico puede girar en ambos sentidos por medio de dos (2) contactores: “D” para el giro a derecha e “I” para el giro a la izquierda. Estos dos contactores son comandados por dos pulsadores de giro “d” (derecha) e “i” (izquierda) y un interruptor de selección “L” de acuerdo con las siguientes condiciones: 

Si solo se pulsa uno de los botones de giro, el motor gira en el sentido correspondiente. 

Si se pulsan los dos botones de giro simultáneamente, el sentido de giro depende del estado del interruptor “L” de forma que:

  Si “L” está activado, el motor gira a la derecha

  Si “L” está en reposo, el motor gira a la izquierda.

...................................................................................................................................................

Diseñar el sistema a que aparece en la figura dada, constituido por cuatro interruptores a, b, c y d, en cuyas posiciones de activados introducen un nivel 1 a las respectivas entradas del bloque A. 

Las salidas del bloque A cumplen las siguientes normas: 

·F1 se activa con 1 cuando existen dos interruptores no contiguos que estén desactivados.

·Por razones de seguridad, si a=1, b=0, c=0, d=1, entonces F1 = 1 y también a=0, b=1, c=1, d=0, entonces F1=0. 

·F2 se activa con 1 cuando hay dos o más interruptores activados. 

·F3 se activa con 1 cuando hay alguno de los interruptores extremos activados. 

Las salidas del bloque A se encuentran conectadas a tres pequeños pilotos P1, P2 y P3. 

...............................................................................................................................................

VIDEO: MAPAS DE KARNAUGH
https://youtu.be/uHbz1TlJEIY

URL: https://www.youtube.com/watch?v=uHbz1TlJEIY

..............................................................................................................................................

TALLER MAPAS DE KARNAUGH

......................................................................................................................................................

CIRCUITOS COMBINACIONALES:

DISEÑO MULTIPLICADOR DE DOS BITS

DISEÑO COMPARADOR

deCODIFICADORES

Un decodificador es un circuito integrado por el que se introduce un número y se activa una y sólo una de las salidas, permaneciendo el resto desactivadas (n entradas y un número de salidas igual o menor a 2n).

DECODIFICADORES CON HABILITACIÓN

deCODIFICADORES BCD A DECIMAL

Los DECODIFICADORES pueden ser de dos tipos:

• No Excitadores. Se denominan así a un tipo de decodificadores cuyas salidas solo pueden acoplarse a otros circuitos digitales de la misma familia integrada, ya que dan una corriente muy pequeña en dichas salidas, incapaz de activar ningún otro componente. Son generadores de funciones lógicas.

• Decodificadores Excitadores. Son aquellos cuyas salidas dan suficiente corriente como para acoplarse, no solo a los circuitos integrados de la misma familia, sino también a otros dispositivos, tales como displays, lámparas, relés, transductores,...

Un decodificador muy común es el de siete segmentos, este circuito combinacional activa simultáneamente varias salidas, decodifica la información de entrada en BCD a un código de siete segmentos adecuado para que se muestre en un display de siete segmentos, es el procedimiento empleado en las calculadoras, los relojes digitales, fuentes de voltaje, etc.

CODIFICADORES

LOS CODIFICADORES permiten "compactar" la información, generando un código de salida a partir de la información de entrada: Codificación de un teclado; Codificador con prioridad; Codificador decimal-BCD; Codificador octal-binario.

CODIFICADOR CON PRIORIDAD: Si se activan 2 entradas al mismo tiempo, sólo sale la que tiene el valor decimal más alto.

CODIFICADOR SIN PRIORIDAD: Si se activan 2 entradas al mismo tiempo, NO se sabe qué valor se emitirá.

MULTIPLEXORES

Los multiplexores , selectores de datos o MUX, son circuitos que permiten seleccionar el paso de una de n señales de entrada. El equivalente mecánico que describe muy bien este comportamiento: es el interruptor de varias posiciones o el interruptor de varias posiciones, de modo que, colocando el selector en una de las posibles entradas, este aparecerá en la salida.

Los multiplexores son circuitos combinacionales con varias entradas y una salida de datos, y están equipados con entradas de control capaces de seleccionar una, y sólo una, de las entradas de datos para permitir su transmisión desde la entrada seleccionada a la salida única.

La entrada seleccionada está determinada por la combinación de ceros lógicos (0) y unos (1) en las entradas de control. El número de entradas de control requeridas será igual a la potencia de 2 que resulte del análisis del número de entradas. 

Tipos de multiplexores

Multiplexor de 2 entradas

Multiplexor de 4 entradas

Multiplexor de 8 entradas

Multiplexor de 16 entradas

Doble multiplexor de 4 entradas